François Chollet works in the field of Artificial Intelligence. He created the Keras library for machine learning and has launched the ARC Challenge for measuring general intelligence.
A definition of general intelligence
In 2019, Chollet published a paper where he defines artificial general intelligence as follows:
The intelligence of a system is a measure of its skill-acquisition efficiency over a scope of tasks, with respect to priors, experience, and generalization difficulty.
This definition focuses on human-like intelligence and uses insights from the field of psychometrics to design an intelligence test for human and non-human agents.
The field of psychometrics is now a well-established discipline, and its findings about the measurement of human intelligence are reliable. The same cannot be said for the state of the art in measuring intelligence of artificial systems.
Difficulties evaluating intelligence of systems
The conditions under which intelligence tests are carried out on humans are not easily transferable to systems.
When evaluating human intelligence, it’s not expected that the human will train for the test; however, that’s the current paradigm for evaluating systems. Developers provide as many examples as possible during a “training phase” so the system can learn and perform well in a final evaluation.
It’s difficult to build a test for systems that cannot easily be exploited – by the use of shortcuts – leading to a high score but in which the system does not show the type of intelligence the test is set to measure. As Chollet puts it:
… optimizing for a single metric or set of metrics often leads to tradeoffs and shortcuts … (a well-known effect on Kaggle, where winning models are often overly specialized for the specific benchmark they won and cannot be deployed on real-world versions of the underlying problem).
Measuring intelligence
Many of the approaches used to measure intelligence focus solely in the performance of an system in a single task, or a set of closely related tasks, Chollet argues that in order to measure general intelligence it is necessary to measure not only the skill of the system at a particular task, but it’s ability to deal properly with new – previously unknown – tasks.
The goal is to measure an system’s broad abilities instead of task-specific skills.
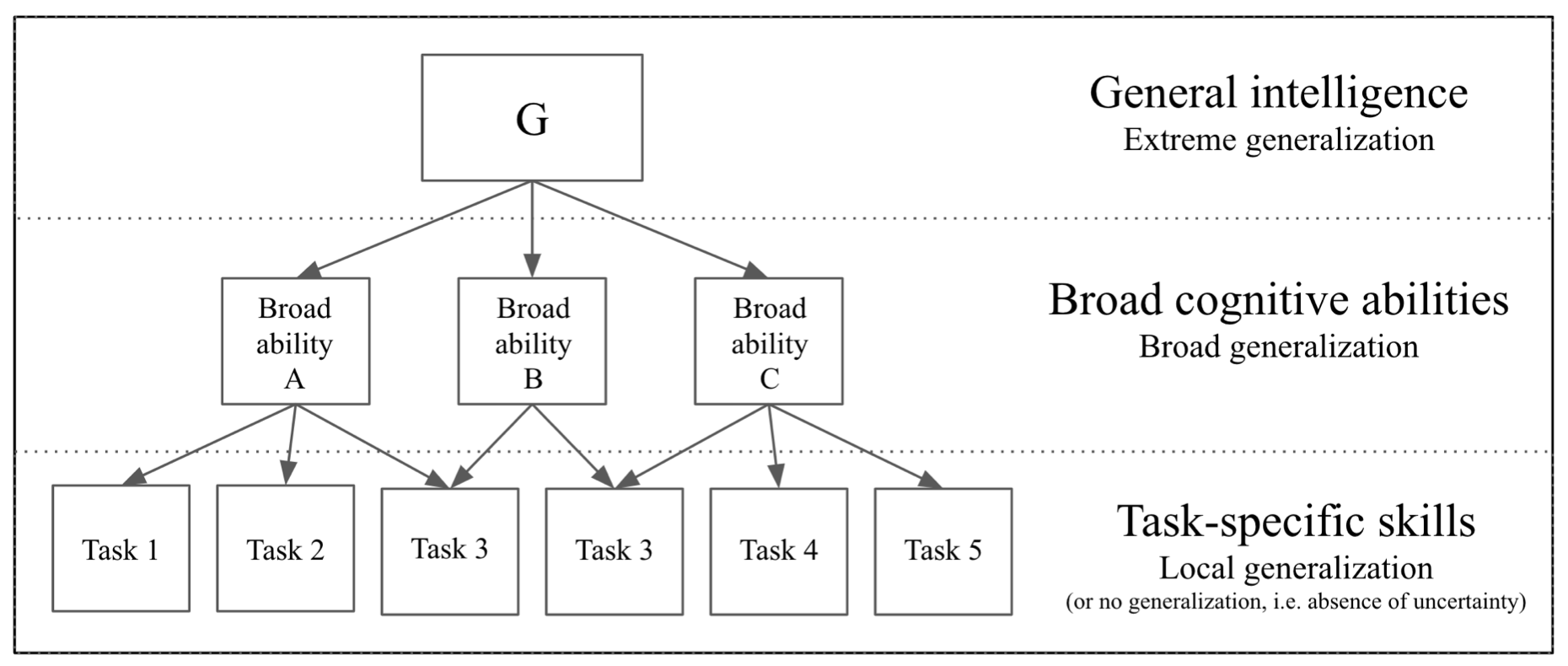
By measuring abilities the emphasis is on the system’s capacity for generalization, that is, the ability to deal with related tasks it’s never seen before, or completely unrelated tasks. Systems that can learn new skills more efficiently can be said to be more intelligent.
Priors: controlling what the system knows
To get human-like intelligence, some assumptions have to be built-in. This will help the system learn certain skills faster. These assumptions are the system’s priors.
By controlling the priors it’s possible to define what the system knows about the environment. In humans, these priors allow them to acquire specific categories of abilities very efficiently.
Controlling priors is also a way to direct what kind of skills the system should learn more efficiently. If no priors were given, the system would have to learn the structure of the environment and there’s no guarantee that the skills acquired would be useful in a human-centric context.
According to Chollet, this anthropocentrism is legitimate and necessary because it’s the only scope we can meaningfully approach and asses.
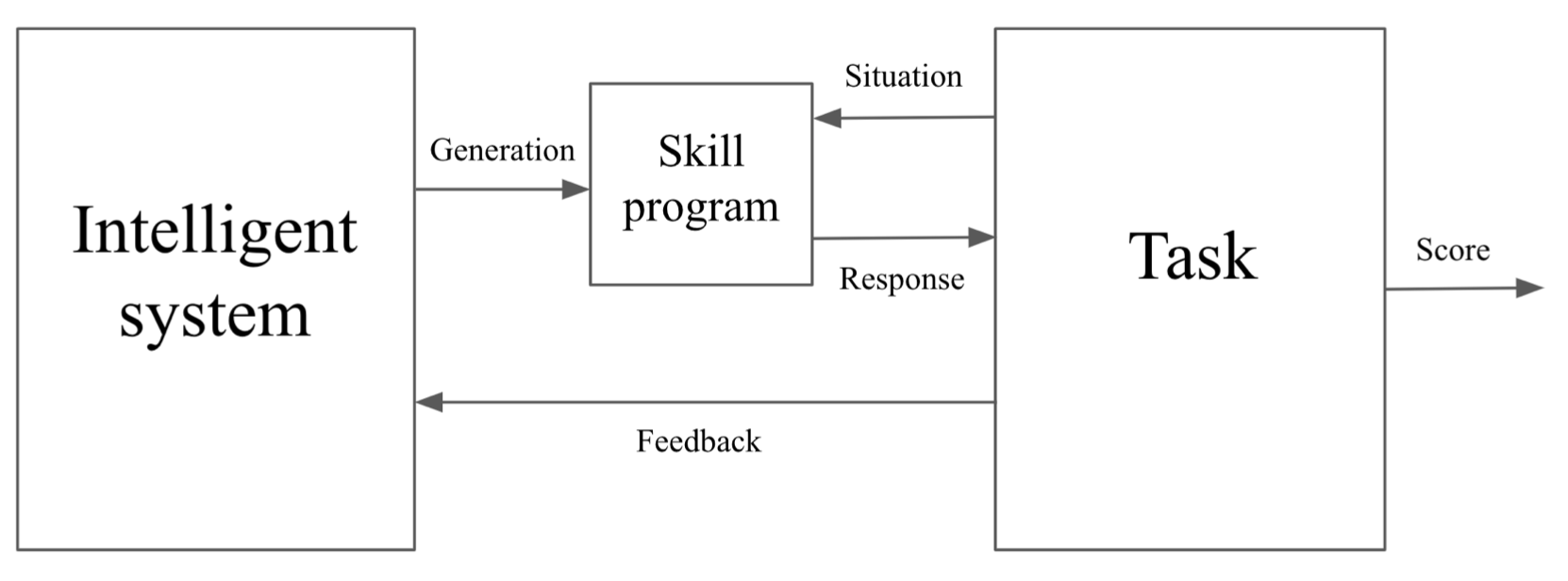
Skill acquisition as program synthesis
During it’s lifetime, a system will face many situations in which it is required to solve a particular task, it does so by generating a skill program.
The system is evaluated and rewarded when it is able to produce program that achieves an acceptable performance solving the task.
The intelligence of the system is directly connected to its ability to generate sufficiently good task-specific skill programs for the given tasks.
Quantifying the intelligence of a system
In the optimal case (\( opt \)), the intelligence \( I \) of a system \( IS \) over a scope \( scope \) is:
\[ I^{opt}_{IS, scope} = \underset{T \in scope}{Avg} \left[ \omega_{T,\Theta} \cdot \Theta \sum_{C \in Cur_T^{opt}} \left[ P_C \cdot \dfrac{ GD_{IS,T,C}^\Theta }{ P_{IS,T}^{\Theta} + E_{IS,T,C}^\Theta } \right] \right] \label{eqn:intelligence} \tag{1} \]
Not all tasks are equal, some are more relevant to humans, some are easier to learn, some are not learnable by the system. To reflect this a weighted average \( \underset{T \in scope}{Avg} \) is used to account for the contribution of each task \( T \) that is in the scope of the system.
The weights \( \omega_{T, \Theta} \) represent how important it is to produce the skill program that can solve task \( T \) with maximum performance \( \Theta \).
The series of interactions the system has with a task is called a Curriculum. There may be different ways of training the system such that it results in optimal performance; the set of such curricula is \( Cur_{T}^{opt} \).
The chances to see a particular curriculum \( C \) during a system’s lifetime is given by \( P_C \). How much a system \( IS \), is able to generalize and reach optimal performance \( \Theta \) depends on the curriculum \( C \) for the given task \( T \), this is called Generalization Difficulty, \( GD_{IS, T, C}^\Theta \).
The knowledge of the system is composed of its priors – its built-in assumptions – and the experience it acquired during training. How strongly the priors contribute to solving task \( T \) optimally is measured with \( P_{IS}^\Theta \). Similarly, the experience gained during training is quantified by \( E_{IS, T, C}^\Theta \).
From the ratio of generalization difficulty to the agent’s previous knowledge we can see that if the prior knowledge is big, then a system that performs optimally at a task would be considered less smart than another system with less prior knowledge that also performs optimally for the same task. Also, if the generalization difficulty is high, a system that solves the task can be said to show more intelligence than another system with the same prior knowledge but solving a task with a lower generalization difficulty.
Task-specific intelligence
An important takeaway is the idea that intelligence can only be measured when a system solves a task. The same system may show little or no intelligence if the task is too easy or out of its scope.
References
- arXiv:1911.01547v2: François Chollet, On the Measure of Intelligence
